Tìm kiếm tam phân - Ternary Search

Tìm kiếm tam phân - Ternary Search¶

Nguồn: e-maxx

Người dịch: Đỗ Thanh Lam

Mở đầu¶

Cho một hàm F(x) chỉ có một cực trị duy nhất (unimodal). Có hai dạng hàm F(x) cơ bản:

Phần đầu tăng chặt, đạt đến giá trị lớn nhất, sau đó giảm chặt. (concave)

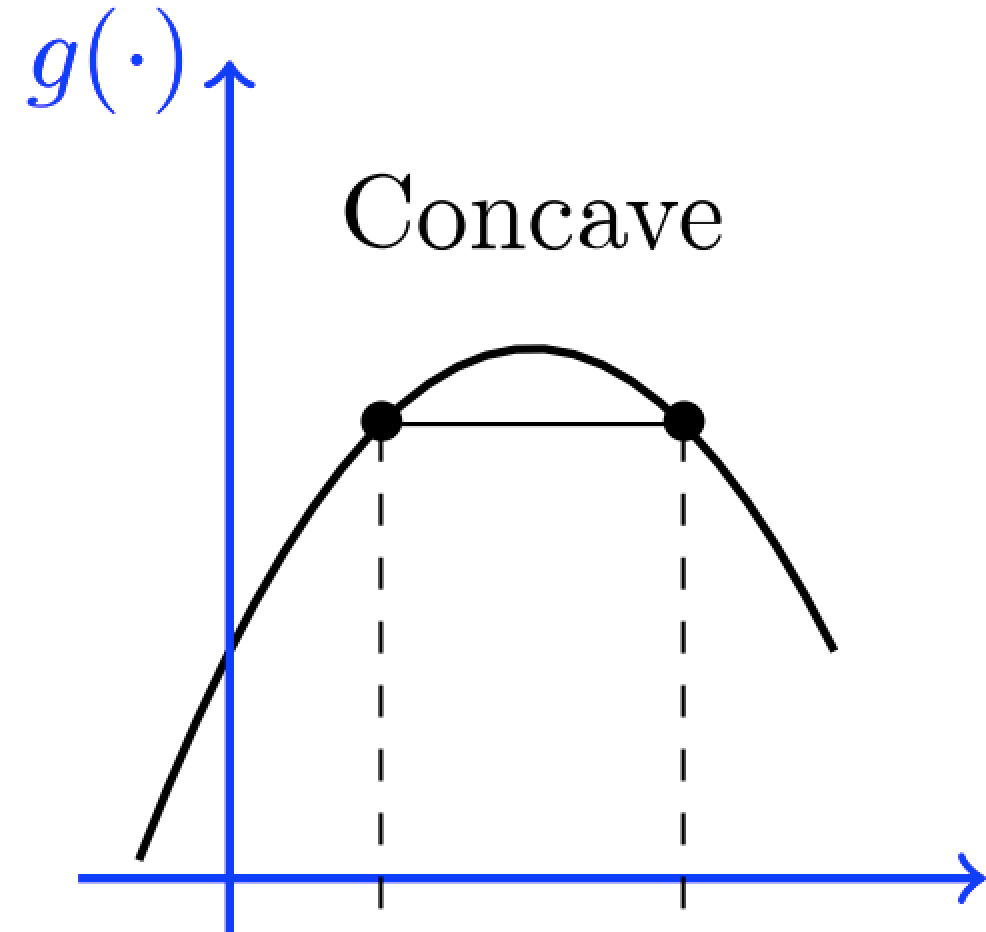
Một hàm số thoả mãn tính chất này nếu tất cả các đoạn thẳng nối 2 điểm của đồ thị hàm số, nằm "bên dưới" của đồ thị.

Phần đầu giảm chặt, đạt đến giá trị nhỏ nhất, sau đó tăng chặt. (convex)

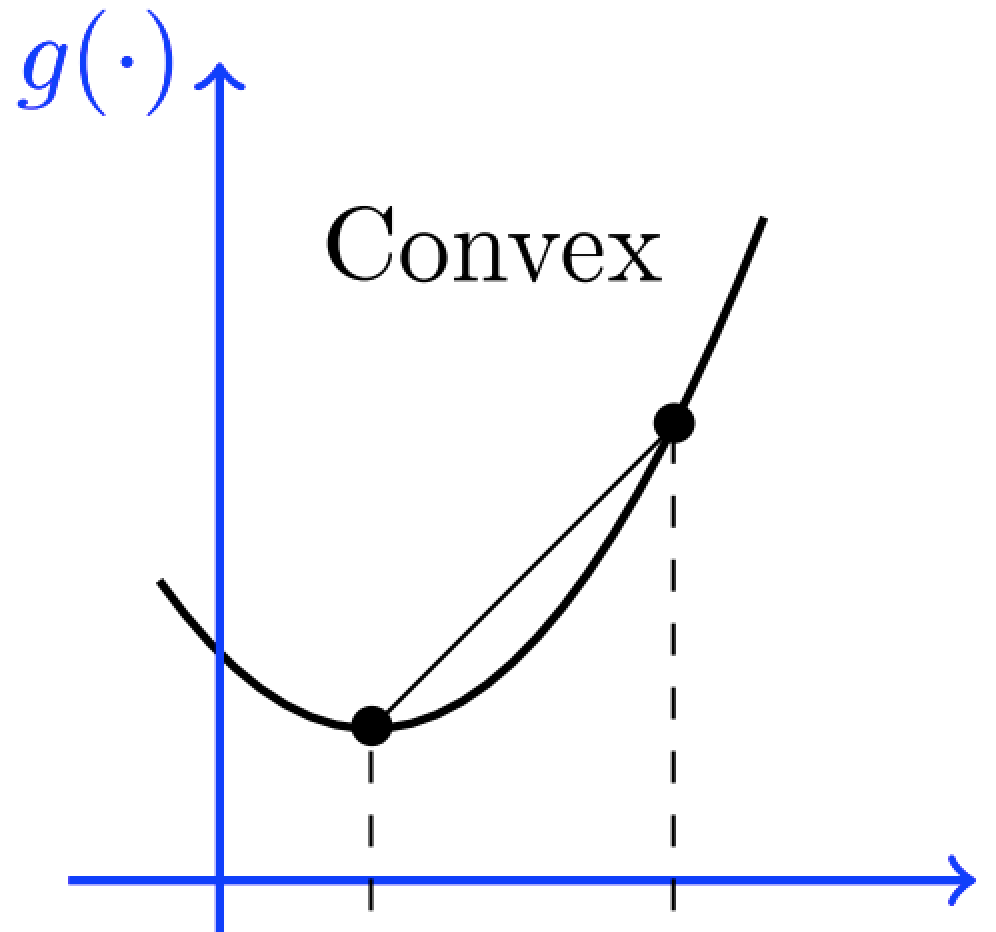
Một hàm số thoả mãn tính chất này nếu tất cả các đoạn thẳng nối 2 điểm của đồ thị hàm số, đều nằm "bên trên" của đồ thị.

Trong bài viết này chúng tôi sẽ giải quyết trường hợp 1, trường hợp 2 sẽ làm tương tự nhưng ngược lại.

Bài toán¶

Cho một hàm \(F(x)\) trong đoạn \([l, r]\) thoả mãn: \(F\) tăng chặt tới một cực đại (điểm H) rồi giảm chặt. Yêu cầu tìm điểm đạt giá trị lớn nhất (điểm H).

Thuật toán¶

Xét hai vị trí \(m_1\) và \(m_2\) trong đoạn \([l, r]\) sao cho \(l < m_1 < m_2 < r\). Rõ ràng cực trị có thể nằm ở 1 trong 3 phần:

\([l, m_1]\). Khi đó, ta biết chắc chắn \(F(m_1) > F(m_2)\).

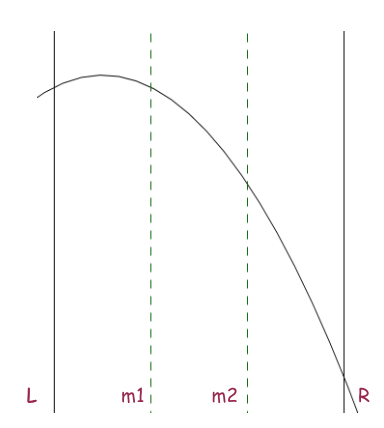
/uploads/ternary_search_case_1.png

\([m_1, m_2]\). Ta không thể rút ra kết luận gì về \(F(m_1)\) và \(F(m_2)\).

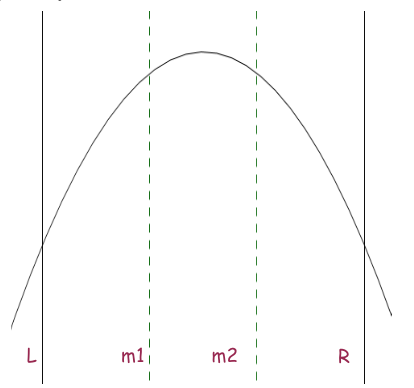
/uploads/ternary_search_case_2.png

\([m_2, R]\). Tương tự trường hợp đầu, ta biết chắc chắn \(F(m_1) < F(m_2)\).

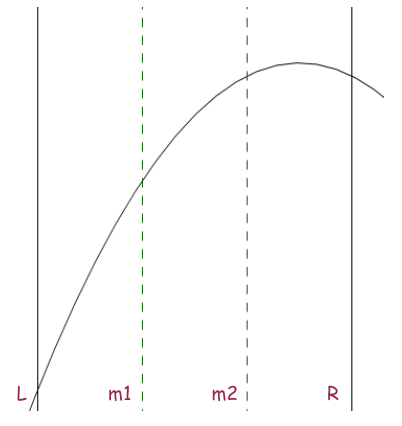
/uploads/ternary_search_case_3.png

Ngược lại, bằng việc so sánh \(F(m_1)\) và \(F(m_2)\), ta có thể rút ra kết luận như sau:

Nếu \(F(m_1) < F(m_2)\): Ta biết chắc chắn H nằm trong \([m_1, r]\).
\(F(m_1) > F(m_2)\): Ta biết chắc chắn H nằm trong \([l, m_2]\).
\(F(m_1) = F(m_2)\): H nằm trong \([m_1, m_2]\). (Chú ý: khi cài đặt chặt tam phân với hàm số thực, ta thường bỏ qua trường hợp này, để tránh sai số, và do trên thực tế 2 số thực hầu như không bao giờ bằng nhau).

Do đó, dựa vào việc so sánh \(F\) ở hai điểm m1, m2 ta có thể thay đổi và giảm không gian tìm kiếm \([l, r]\) xuống một khoản không gian nhỏ hơn \([l', r']\). Nếu ta chọn:

\(m_1 = l + (r - l) / 3\)
\(m_2 = r - (r - l) / 3\)

Thì sau mỗi lần, độ lớn của đoạn \([l, r]\) giảm xuống còn \(2/3\) lần.

Nếu ta lặp đi lặp lại K lần, thì độ lớn của [l, r] sẽ chỉ còn \((2 / 3) ^ K\). Ví dụ với \(l = -10^9, r = 10^9\), ta lặp lại \(K = 100\) lần, thì đoạn [l, r] thu về chỉ còn độ dài là \((2 / 3.0) ^ {100} * (2*10^9) < 5 * 10^{-9}\), đủ chính xác với hầu hết mọi bài toán.

Độ phức tạp thuật toán là \(O(logT)\) với T là độ chính xác mà ta cần thực hiện.

Cài đặt¶

double max_f(double left, double right) {

    int N_ITER = 100;

    for (int i = 0; i < N_ITER; i++) {

        double x1 = left + (right - left) / 3.0;
        double x2 = right - (right - left) / 3.0;

        if (f(x1) > f(x2)) right = x2;
        else left = x1;
    }
    return f(left);
}

Mở rộng¶

Tìm kiếm tam phân cũng có thể dùng để giải các bài toán trên 2D với hàm dạng \(f(x, y)\) nếu hàm f là hàm lồi. Ví dụ bài E trong đề ACM ICPC Vietnam National Round 2017, lời giải chi tiết ở đây.

Tìm kiếm tam phân - Ternary Search