Bài toán LUBENICA

Thuật toán

Bài này có nhiều hướng giải, một trong số đó là sử dụng kỹ thuật Heavy Light Decomposition, tuy nhiên có 1 cách làm đơn giản hơn cho bài này là sử dụng LCA và RMQ

Giải bằng LCA

Gọi up[u][i].par là tổ tiên thứ \(2^i\) của \(u\), maxc là cạnh có trọng số lớn nhất trên đường đi từ u lên up[u][i]. Tương tự với minc là cạnh có trọng số nhỏ nhất. Có thể tính \(up[u][0]\) khi dfs dựng cây, tức là nút cha trực tiếp của u, cũng là cạnh từ cha đến u. Có thể tính up[u][i] (i > 0) thông qua công thức QHĐ sau:

Đặt p = up[u][i-1].par, do p là cha thứ \(2^i\) của \(u\) ⇒ up[u][i].par = up[p][i-1].par , cha thứ \(2^{i-1}\) của p cũng là cha thứ \(2^i\) của u.

Vậy nên up[u][i].maxc = max(up[u][i-1].maxc. up[p][i-1].maxc) có nghĩa là trọng số lớn nhất khi nhảy từ u lên cha thứ \(2^i\) đi qua các cạnh bằng trọng số lớn nhất khi nhảy từ u lên cha thứ \(2^{i - 1}\) là p và nhảy từ p lên cha thứ \(2^{i - 1}\)

Ví dụ : Với u = 10, i = 2 ta thực hiện cập nhật mảng up như hình vẽ dưới đây:

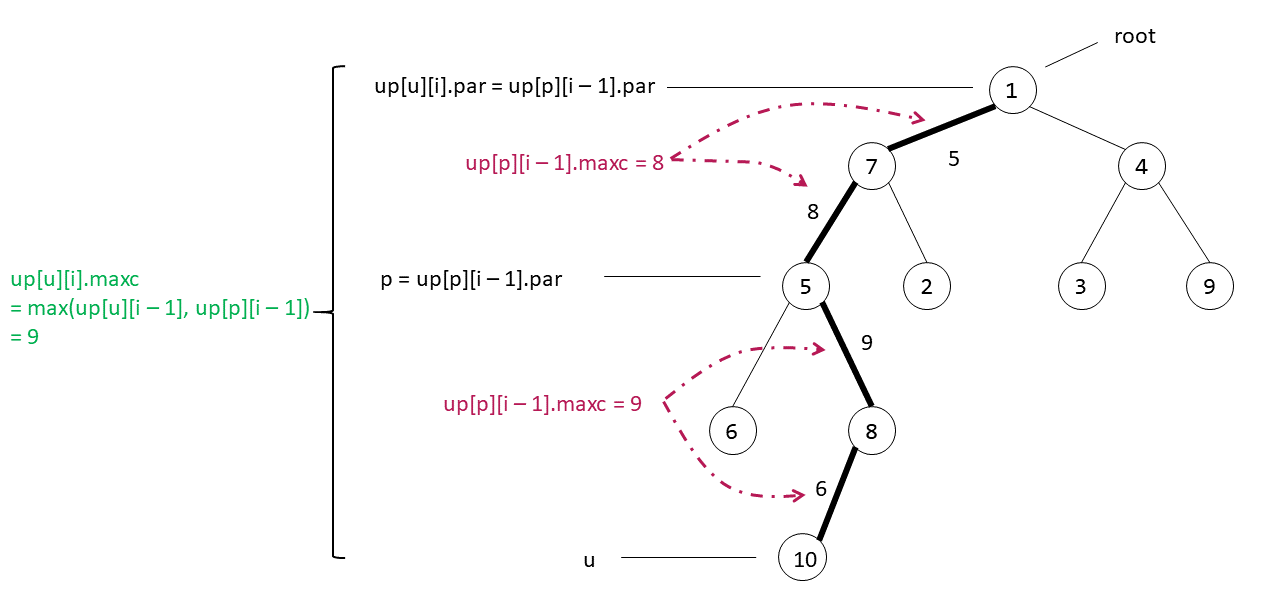
• up[u][i - 1].maxc ở đây là trọng số lớn nhất của các cạnh 5 - 8 và 8 - 10, do đó có giá trị bằng 9
• up[p][i - 1].maxc ở đây là trọng số lớn nhất của các cạnh 1 - 7 và 7 - 5, do đó có giá trị bằng 8 Khi đó up[u][i].maxc ta sẽ cập nhật bằng giá trị lớn nhất của up[u][i - 1].maxc và up[p][i - 1].maxc có nghĩa là khi nhảy từ u = 10 lên cha thứ \(2^{i - 1}\) là p = 5 và từ p lên cha thứ \(2^{i - 1}\) của p là 1. Nên up[u][i].maxc = max(8, 9) = 9.

Tương tự cho min. Sau đó với mỗi truy vấn tìm LCA của hai đỉnh rồi tìm min và max trên mỗi đoạn này

Code mẫu

## include <bits/stdc++.h>
using namespace std;
## define fi first
## define se second
## define bit(x, k) (1ll&((x) >> (k)))

const int N = 1e5 + 11;
const int INF = 1e9 + 11;

struct Data {
    int par, minc = INF, maxc = -INF;
};

int n, q, h[N];
Data up[N][21];
vector < pair<int, int> > g[N];

void dfs(int u, int p) { // xây dựng mảng up, mảng h
    up[u][0].par = p;
    for (auto &e : g[u]) {
        int v = e.fi; int c = e.se;
        if (v == p) continue;
        h[v] = h[u] + 1; // độ sâu của nút v
        up[v][0].maxc = up[v][0].minc = c;
        dfs(v, u);
    }
}

void solve(int u, int v) {
    Data res;
    // mặc định u có độ sâu lớn hơn v
    if (h[u] < h[v]) swap(u, v);
    int depth = h[u] - h[v];
    // từ u nhảy lên cha có cùng độ sâu với v đồng thời cập nhật max, min các cạnh
    for (int i = 20; i >= 0; i--) {
        if (bit(depth, i)) {
            res.maxc = max(res.maxc, up[u][i].maxc);
            res.minc = min(res.minc, up[u][i].minc);
            u = up[u][i].par;
        }
    }

    // u bằng v thì in ra kết quả
    if (u == v) {
        cout << res.minc << ' ' << res.maxc << '\n';
        return;
    }
    // u và v nhảy đồng thời lên cha chung gần nhất và cập nhật
    for (int i = 20; i >= 0; --i) {
        if (up[u][i].par != up[v][i].par) {
            res.maxc = max({res.maxc, up[u][i].maxc, up[v][i].maxc});
            res.minc = min({res.minc, up[u][i].minc, up[v][i].minc});
            u = up[u][i].par; v = up[v][i].par;
        }
    }
    res.maxc = max({res.maxc, up[u][0].maxc, up[v][0].maxc});
    res.minc = min({res.minc, up[u][0].minc, up[v][0].minc});
    cout << res.minc << ' ' << res.maxc << '\n';
}

void buildLCA() {
    dfs(1, 1);
    for (int i = 1; i <= 20; i++) {
        for (int u = 1; u <= n; u++) {
            up[u][i].par = up[up[u][i - 1].par][i - 1].par;
            up[u][i].maxc = max(up[u][i - 1].maxc, up[up[u][i - 1].par][i - 1].maxc);
            up[u][i].minc = min(up[u][i - 1].minc, up[up[u][i - 1].par][i - 1].minc);
        }
    }
}

int main() {
    ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);

    cin >> n;
    for (int i = 1; i <= n - 1; i++) {
        int u, v, c;
        cin >> u >> v >> c;
        g[u].push_back({v, c});
        g[v].push_back({u, c});
    }

    buildLCA();

    cin >> q;
    while (q--) {
        int u, v;
        cin >> u >> v;
        // tìm min, max của trọng số các cạnh trên đường đi từ u đến v
        solve(u, v);
    }
    return 0;
}